EPJ Nuclear Sci. Technol. 4, 15 (2018)
https://doi.org/10.1051/epjn/2018019

Regular Article

Efficient use of Monte Carlo: the fast correlation coefficient

¹ Department of Physics and Astronomy, Uppsala University, Uppsala, Sweden
² Nuclear Research and Consultancy Group NRG, Petten, The Netherlands
³ Reactor Physics and Thermal Hydraulic Laboratory, Paul Scherrer Institut, Villigen, Switzerland

^* e-mail: henrik.sjostrand@physics.uu.se

Received: 16 January 2018
Received in final form: 16 February 2018
Accepted: 4 May 2018
Published online: 29 June 2018

Abstract

Random sampling methods are used for nuclear data (ND) uncertainty propagation, often in combination with the use of Monte Carlo codes (e.g., MCNP). One example is the Total Monte Carlo (TMC) method. The standard way to visualize and interpret ND covariances is by the use of the Pearson correlation coefficient, $$\rho =\frac{cov(x,y)}{{\sigma }_x\times {\sigma }_y},$$

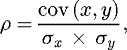
where x or y can be any parameter dependent on ND. The spread in the output, σ, has both an ND component, σ_ND, and a statistical component, σ_stat. The contribution from σ_stat decreases the value of ρ, and hence it underestimates the impact of the correlation. One way to address this is to minimize σ_stat by using longer simulation run-times. Alternatively, as proposed here, a so-called fast correlation coefficient is used, $${\rho }_{\text{fast}}=\frac{cov(x,y)-cov(x_{\text{stat}},y_{\text{stat}})}{\sqrt{{\sigma }_x^2-{\sigma }_{x,\text{stat}}^2}·\sqrt{{\sigma }_y^2-{\sigma }_{y,\text{stat}}^2}}.$$

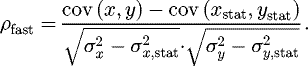
In many cases, _cov(x_stat; y_stat) can be assumed to be zero. The paper explores three examples, a synthetic data study, correlations in the NRG High Flux Reactor spectrum, and the correlations between integral criticality experiments. It is concluded that the use of ρ underestimates the correlation. The impact of the use of ρ_fast is quantified, and the implication of the results is discussed.